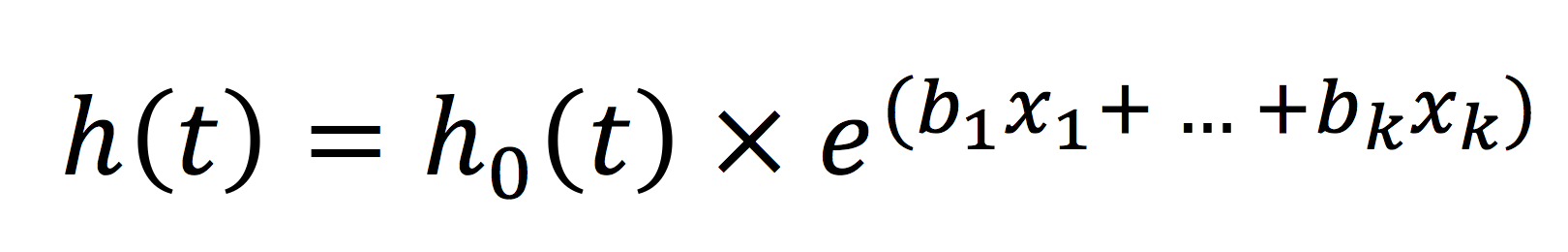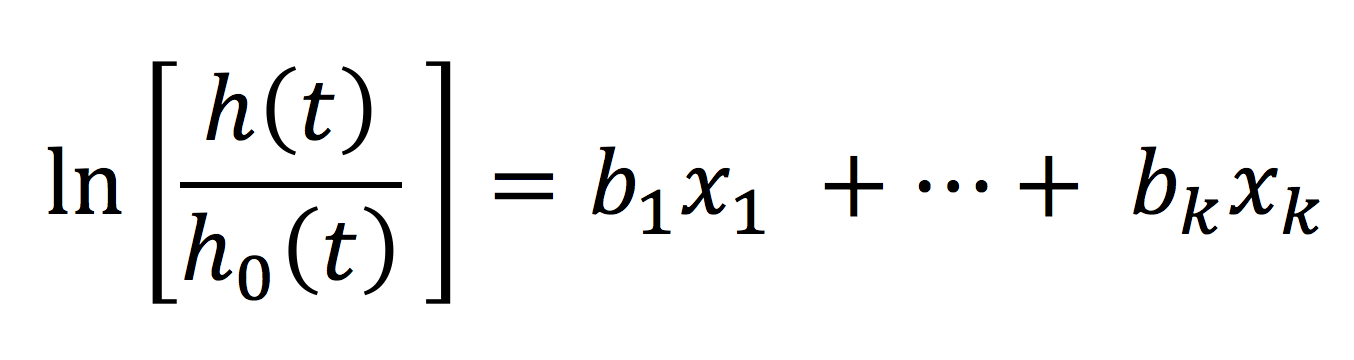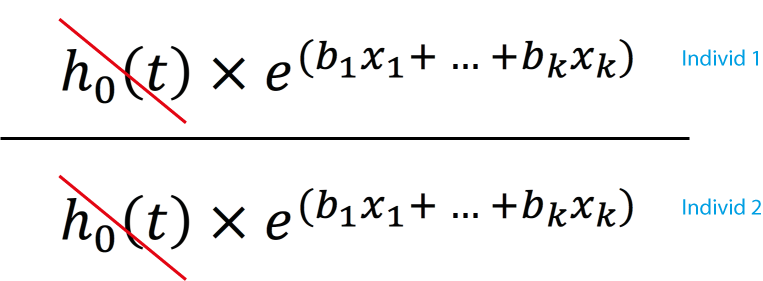Överlevnadsanalys: Kaplan-Meier till Cox regression
Överlevnadsanalys (survival analysis)– Från Kaplan-Meier till Cox regression
En reviderad version av detta kapitel finns här:
Överlevnadsanalys är ett kraftfullt verktyg för att studera händelser (events). Centralt för överlevnadsanalys är information om observationstid. Man studerar nämligen alltid tid till att en händelse inträffar. I engelsk litteratur används benämningarna survival analysis eller time-to-event analysis. Den sistnämnda termen, time-to-event analysis, är egentligen mer korrekt eftersom dessa analyser kan användas för att studera alla händelser och inte bara död. I detta kapitel kommer vi dock använda död som exempel eftersom det underlättar förståelsen.
Centralt för överlevnadsanalys är kännedom om observationstid, vilket är tidsperioden då individen observeras. Det behöver givetvis inte vara en person som observeras, det kan lika gärna vara celler, bakterier eller dylikt. I dess renaste form startar observationstiden när individen inkluderas i studien och observationstiden slutar när händelsen inträffar eller när studiens uppföljningsperiod är slut. Tidsperioden då individen observeras kallas survival time.
Syftet med överlevnadsanalys är som följer:
- Studera överlevnadsprocessen.
- Studera hur olika prediktorer påverkar överlevnad.
För att studera överlevnadsprocessen kan man använda deskriptiva metoder, varav den viktigaste är Kaplan-Meier estimatorn (Kaplan-Meier-kurvan). Med Kaplan-Meiers metod får man en grafisk (och matematisk) beskrivning av överlevnaden. Med metoden kan man även jämföra överlevnaden mellan två eller flera grupper. Med Kaplan-Meier estimatorn kan man dock inte göra djupgående analyser av olika prediktorers inverkan på överlevnaden.
För att studera hur olika prediktorer påverkar överlevnaden så krävs regressionsanalys. Idag domineras överlevnadsanalys av Cox regression (Cox Proportional Hazards Model) som gör det möjligt att jämföra överlevnaden mellan två eller flera grupper, samt studera hur olika prediktorer påverkar överlevnaden. Cox regression är ett oerhört kraftfullt verktyg och dagligen publiceras tusentals artiklar där Cox regressionen utgör studiens hörnsten.
Kaplan-Meier estimatorn och Cox regression är de viktigaste verktygen att behärska och därför fokuserar den fortsatta diskussionen kring dessa två.
Överlevnadsanalys vs. logistisk regression
Med överlevnadsanalys studeras alltså dikotoma (binära) händelser (events). Man studerar om en händelse inträffar eller uteblir. I det avseende har överlevnadsanalys likheter med logistisk regression (se Logistisk regression). Faktum är att logistisk regression också används för att studera diktoma händelser. Dagligen publiceras hundratals artiklar där logistisk regression använts för att studera samband mellan diverse prediktorer och död och andra events. Logistisk regression är dock (i princip) alltid ett sämre val än överlevnadsanalys för att studera survival och detta beror på att logistisk regression inte kan beakta observationstiden. Själva observationstiden är nyckeln till överlevnadsanalysen (det är faktiskt survival time distributionen som studeras vid överlevnadsanalys) och den kan inte inkorporeras i en logistisk regression. Låt oss illustrera detta med ett (extremt) exempel:
Du studerar effekten av ett läkemedel som gavs till 50 av 100 patienter med lungcancer under år 2013. Dessa patienter följdes upp år 2014 och då var samtliga patienter döda. Lika många dör alltså bland de som fick respektive inte fick läkemedlet. Du genomför en logistisk regression där överlevnad granskas (som ett dikotomt utfall) under 2014. Eftersom alla patienter är döda så kommer den logistiska regressionen indikera att läkemedlet är effektlöst eftersom antalet döda vid 2014 var lika många i båda grupperna. Låt oss säga att medianöverlevnaden i gruppen som inte fick läkemedel var 1 månad och gruppen som fick läkemedlet hade medianöverlevnad på 6 månader. Alla var förvisso döda efter 12 månader men det tycks ändå vara så att läkemedlet förlängde livet. Med korrekt överlevnadsanalys skulle vi kunna bekräfta att läkemedlet är effektivt och detta beror på att överlevnadsanalysen kan inkorporera själva överlevnadstiden (survival time)!
Med överlevnadsanalys (och i synnerhet Cox regression) har man alltså större chans att hitta skillnader i överlevnad. Man bör alltid föredra överlevnadsanalys (särskilt Cox regression) framför logistisk regression om man har uppgift om survival time. (Det kan dock nämnas att under särskilda omständigheter kan logistisk regression vara ekvivalent med Cox regression men det diskuteras inte i detta kapitelet).
Event (outcome, utfallsmått, händelsen) i överlevnadsanalys
Utfallet i en överlevnadsanalys är en händelse (engelska: event). Händelsen kan vara död, insjuknande i stroke, cancerdiagnos eller mjukare events såsom insättning av läkemedel eller utskrivning från sjukhus. Man kan alltså studera alla typer av händelser med överlevnadsanalys. Det inkluderar även livslängden på en dator. Själva händelsens natur är alltså av underordnad betydelse men det är undersökarens ansvar att definiera en tydlig och meningsfull händelse. Alla personer som ingår i populationen skall följas från tidpunkten då de inkluderas i studien tills uppföljningen är slut. Det är viktigt att kunna datera (med så hög precision som möjligt) tidpunkt för händelsen, så att observationstiden kan beräknas med hög upplösning. Det är alltså mycket bättre att registrera survival time i antal dagar istället för antal månader. Ju grövre mått på survival time desto sämre precision i analysen.
Prediktorer, kovariater & oberoende variabler
När överlevnadsanalys används för att studera hur olika variabler påverkar utfallet så görs det vanligtvis med Cox regression (Cox proportional hazards model). De variabler som studeras kallas prediktorer, kovariater eller oberoende variabler. Samtliga dessa tre benämningar kan användas och de syftar alltså på samma sak.
Censoring (censurering)
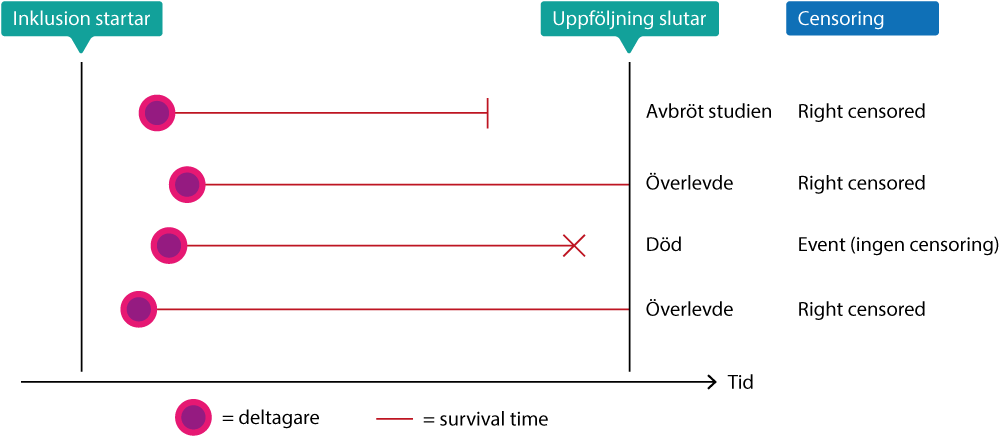
Överlevnadstid (survival time) är en kontinuerlig variabel och det kan därför vara lockande att använda linjär regression för att studera överlevnad. Det är dock inte möjligt att använda linjär regression och detta beror på censurering (eng: censoring). Som regel kommer inte alla personer uppleva händelsen som studeras; det är exempelvis sällsynt att alla personer i studien avlider. De personer som överlever hela observationstiden utgör alltså ett problem eftersom vi inte kan säga om eller när de kommer dö. Dessa personer blir censurerade (eng: censored) när studiens uppföljning slutar. Samma problem uppstår om studiedeltagare hoppar av studien (t ex pga biverkningar av läkemedel, eller för att de flyttar utomlands etc). Dessa personer blir också censurerade (eftersom vi inte kan säga om eller när de kommer dö). Censoring innebär alltså att uppföljningen slutar innan händelsen inträffat. Man skiljer på tre typer av censoring:
- Om en person fullföljer studien utan att händelsen inträffar, så blir personen right censored. Det innebär att vi endast kan uttala oss om patientens öde fram till ögonblicket då uppföljningen slutar. Personer som hoppar av studien (oavsett skäl) blir också right censored.
- Vi är ofta intresserade av en viss exponering; en studie kan exempelvis undersöka hur diabetes påverkar överlevnaden. Ofta är det dock okänt när diabetessjukdomen uppkom. Sjukdomen kan ha förelegat många år innan diagnosen ställdes. Om det är okänt när en exponering startade så är individen left censored i det avseendet. Left censoring innebär alltså att det är oklart när individens risk startade. Detta brukar dock inte vara något större bekymmer.
- Om en individ är både left och right censored, så är den interval censored.
Informativ vs non-informativ censoring
Censoring måste vara oberoende av (1) individens kovariater (prediktorer) och (2) hur långt individen har klarat sig i studien. Censoring under studiens gång (innan uppföljningen är avslutad) skall vara slumpmässig, annars föreligger bias i studien. Ett exempel följer. Ponera att vi studerar effekten av blodtrycksmedicin på död. Det aktuella läkemedlet som studeras visar sig medföra svåra biverkningar, så till vida att många personer som får läkemedlet tvingas hoppa av studien. I det fallet drivs censoring av en kovariat (prediktor), nämligen läkemedlet och då uppstår bias eftersom patienterna hoppar av studien innan de hinner dö. Detta leder till underskattning av antalet dödsfall och därmed överskattning av överlevnad. Den typen av censoring kallas informativ censoring, vilket innebär att censoring inte var slumpmässig.
Censoring skall alltså vara non-informativ, vilket innebär att det inte skall finnas någon anledning till censoring. I exemplet med blodtrycksmedicin så kommer distributionen av survival time vara lika mellan grupperna om censoring är non-informativ.
Survival function och hazard function
Överlevnad (survival time) är en kontinuerlig variabel som kan beskrivas med två enkla funktioner:
S(t) – survival function (överlevnadsfunktion): S(t) är sannolikheten för att en person skall vara vid liv efter tidpunkt t.
h(t) – hazard function (hazardfunktion): h(t) indikerar den omedelbara risken för att händelsen skall inträffa vid tidpunkt t, förutsatt att personen överlevt fram till dess.
Formeln och sambandet mellan S(t) och h(t) är som följer:
S(t) används för att skapa deskriptiv statistik. Genom att hitta beräkna S(t) så kan bland annat överlevnadsgrafer och medianöverlevnad bestämmas. Medianöverlevnaden är tidpunkten då 50% av den ursprungliga kohorten är vid liv, vilket innebär att S(t) = 0.5. Notera att både överlevnadsgrafer och medianöverlevnad rapporteras i flertalet undersökningar med överlevnadsanalys. Hazardfunktionen, däremot, brukar inte presenteras i en vetenskaplig studie. Den har icke desto mindre fundamental betydelse för överlevnadsanalys vilket diskuteras senare.
S(t) och Kaplan-Meier estimatorn (kurvan)
Det är som regel alltid av intresse att visualisera överlevnaden med en graf eftersom det förtäljer hur överlevnadsprocessen ser ut över tid. Om deltagarna huvudsakligen dör i början, i mitten eller slutet av en studie kan skönjas enkelt med en graf. Den vanligaste metoden för att presentera S(t) är med hjälp av Kaplan-Meier estimatorn.
För att skapa en Kaplan-Meier kurva måste tidskalan (uppföljningstiden) brytas ner till interavaller (Figur 2). Varje intervall börjar när ett event inträffar. Alla tidpunkter då händelser inträffar (event times) rangordnas, från första till sista event. Vid t1 inträffar den första händelsen, vid t2 inträffar den andra händelsen, vid t3 inträffar den tredje händelsen och så vidare. Studien börjar vid t0 och då har ännu ingen händelse inträffat. Vid t0 är S(t) = 1.0, vilket innebär att sannolikheten för överlevnad är 100%. För att beräkna S(t) vid t1 så görs följande beräkning:
(n1 – m1) / n1
n1 är antal patienter observerade i början av t1.
m1 är antal events vid t1.
Detta är alltså andelen patienter som överlever efter t1, bland de patienter som överlevde fram till t1.
För att beräkna sannolikheten för att överleva efter t2, förutsatt att man klarar sig fram till dess görs beräkningen i två steg:
(n2 – m2) / n2
n2 är antal patienter observerade i början av t2.
m2 är antal events vid t2.
Vilket alltså är andelen patienter som överlever efter t2, bland de som överlevde fram till t2. S(t) är produkten av sannolikheten att överleva fram till t2, vilket blir:
(n1 –m1)/n1 × (n2 – m2)/n2
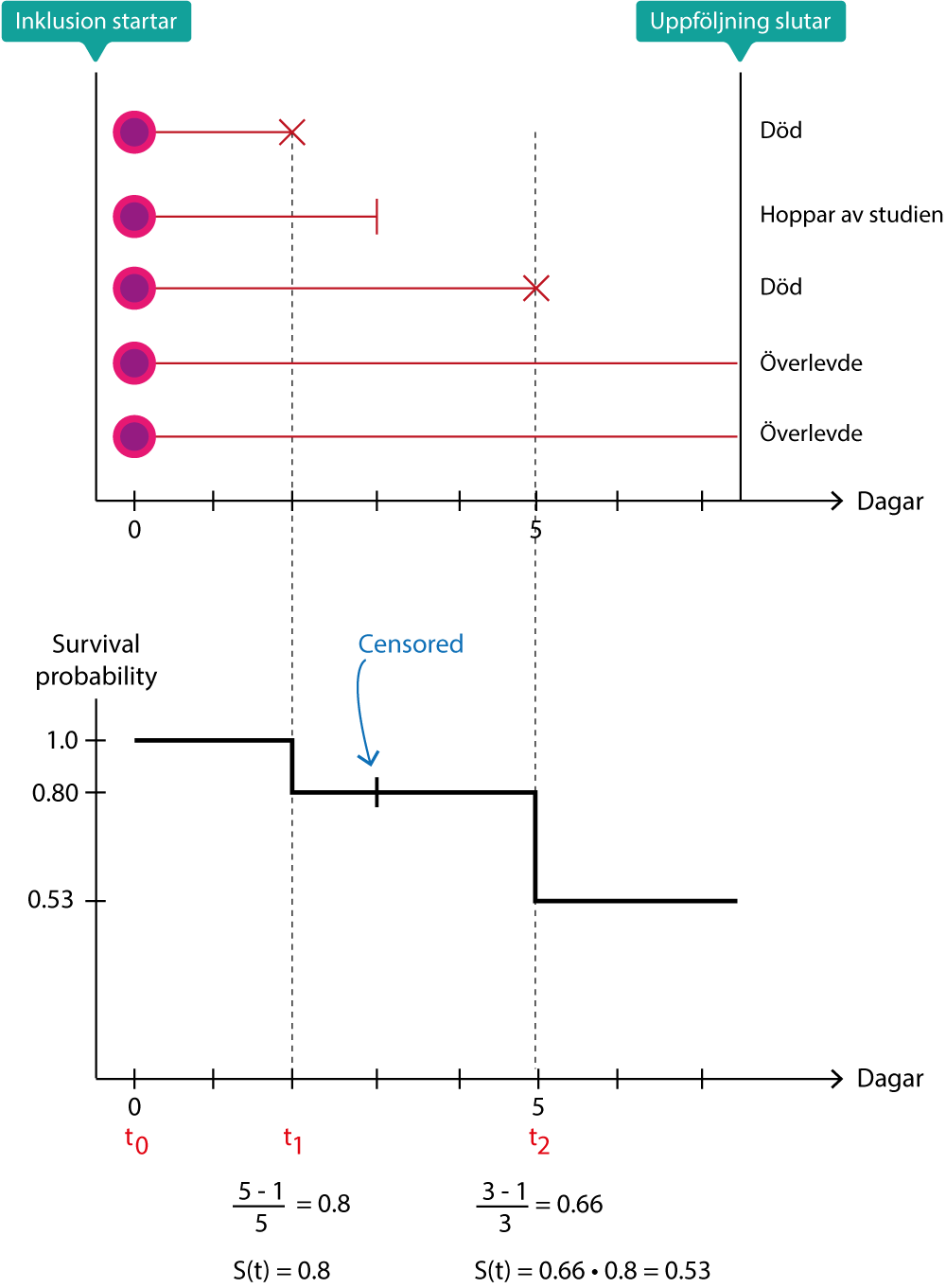
Överlevnadskurvan (Kaplan-Meier-kurvan) visar survival probability på Y-axeln och tid på X axeln. Survival probability är S(t) och det är alltså andelen som fortfarande är vid liv vid varje tidpunkt. Kurvan börjar alltid på Y = 1, eftersom alla överlever fram till t1 (då första eventet inträffar). Därefter går kurvan gradvis nedåt allteftersom folk dör. Eventuella ”+” på kurvan indikerar tidpunkter då personer censureras (dvs uppföljningen slutar innan event inträffar). Som du märker på ovanstående figur så påverkas inte S(t) av censurering. Kaplan-Meier kurvan når endast S(t) = 0 om alla i studien dör. Medianöverlevnaden är helt enkelt andelen som lever vid S(t) = 0.5.
Testa skillnad mellan överlevnadskurvor: log-rank test
I följande figur jämförs överlevnaden mellan män och kvinnor.
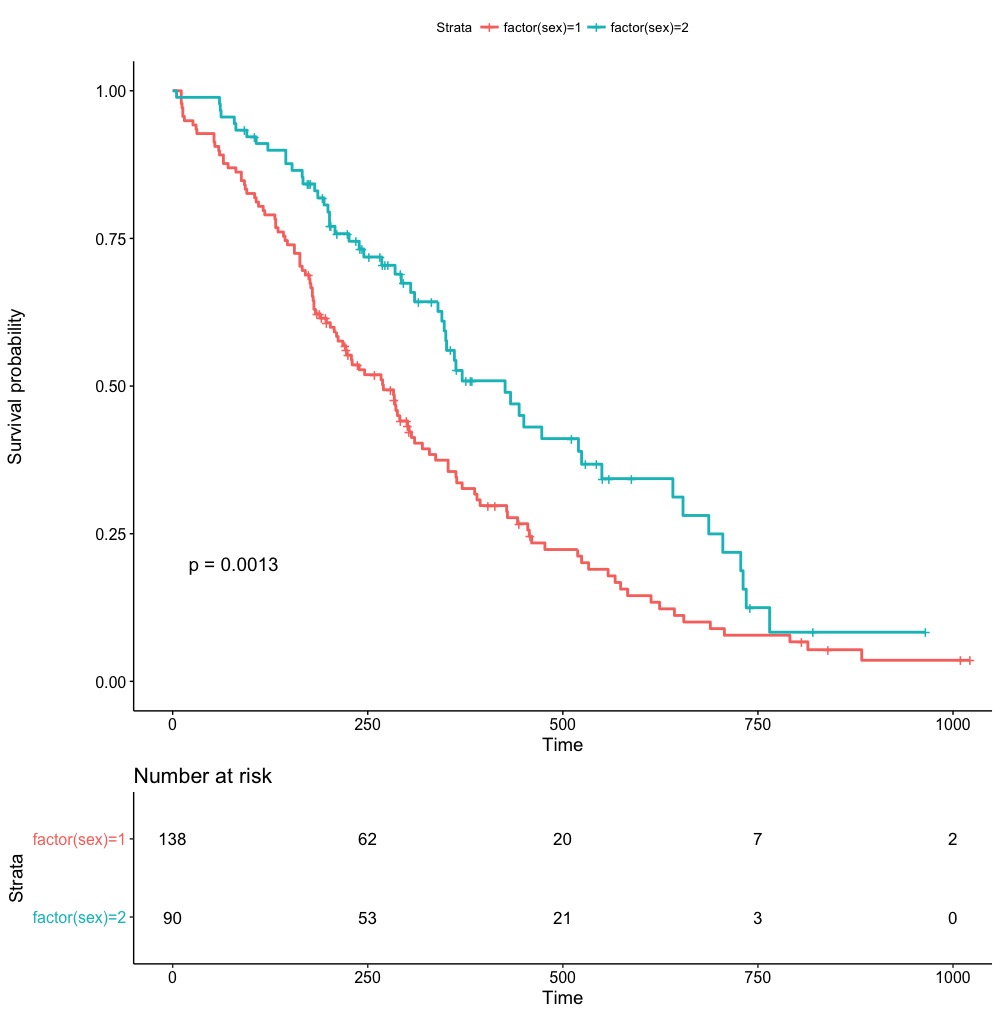
R kod för ovanstående Kaplan-Meier-kurva
install.packages("survival")
library(survival)
install.packages("survminer")
library(survminer)
# Ladda exempeldata och se datastrukturen
data(lung)
str(lung)
# säkerställer att sex är en kategorisk variabel genom att tvinga den till det via funktionen "as.factor"
lung$sex <- as.factor(lung$sex)
# Skapa survfit-objekt. I detta objektet skapas överlevnadsfunktionen
fit <- survfit(Surv(time, status==2) ~ sex, data = lung)
# Rita Kaplan-Meier-kurva
ggsurvplot(fit, data = lung, risk.table = TRUE, pval = TRUE)
Som framgår ovan så är kurvorna separerade, vilket innebär att överlevnaden skiljer sig mellan män och kvinnor. Vid varje tidpunkt är S(t) högre för kvinnor (linjen för kvinnor ligger över linjen för män). Det innebär att överlevnaden är bättre för kvinnor och det kan alltså bedömas visuellt. Det är dock önskvärt att testa om överlevnaden skiljer sig genom att använda ett statistiskt test. För detta ändamål använder man log-rank test.
Principen för log-rank test följer principen för hypotestestning. Man utgår från nollhypotesen som säger att det inte finns någon skillnad mellan grupperna och därefter beräknas en sannolikhet (p-värde) för att nollhypotesen stämmer. Om sannolikheten är <0.05 så förkastas nollhypotesen. Grupperna kan baseras på godtycklig variabel som är kategorisk, med två eller flera kategorier. I exemplet ovan finns endast två grupper, nämligen män och kvinnor. Log-rank-testet kan alltså användas för att jämföra två eller flera överlevnadskurvor.
Således kan Kaplan-Meier-kurvan användas för att studera överlevnad. Detta kan göras i hela populationen eller subgrupper (t ex män och kvinnor). Man kan dock inte justera för kovariater i en Kaplan-Meier-beräkning; detta kräver regressionsanalys.
Cox regression (Proportional Hazards Model)
Idag är Cox regression nästan synonymt med överlevnadsanalys. Detta beror på metodens många fördelar gentemot andra regressionsmodeller. Alternativen till Cox regression, exempelvis Weibull regression, ger under vissa omständigheter mer korrekta parameterestimat men på bekostnad av komplexiteten. Cox regressionen är en enkel och kraftfull modell för att studera överlevnad. Skillnaden mellan Cox regression och Kaplan-Meier-analys är att förstnämnda är just en regressionsmodell, vilket innebär att vi kan studera hur olika prediktorer påverkar överlevnaden. Cox regressioner kan, likt vanlig multipel regression, inkludera en eller flera prediktorer. Cox regression är faktiskt en variant av den linjära modellen, vilket förklaras nedan.
I en Cox regression studeras sambandet mellan prediktorer (kovariater) och survival time. För att anlända till ekvationen för Cox regression tar vi avstamp i hazard function, h(t), och survival function, S(t).
- Hazard function, h(t), för en händelse vid tidpunkt t (alltså en godtycklig tidpunkt) är ekvivalent med event rate (hastigheten med vilken händelser inträffar) för de patienter som ännu inte erfarit händelsen.
- Survival function, S(t), är sannolikheten för att ännu (vid tidpunkt t) inte ha erfarit händelsen.
Det finns ett matematiskt samband mellan h(t) och S(t) och det är som följer:
Cox regressionen utgår från hazard function och definierar följande modell:
h0(t) är baseline hazard och denna kvantitet kan vara aningen krånglig. Baseline hazard är den risk som individen har när värdet på alla prediktorer är 0. Två exempel följer. (1) Föreställ dig att vi studerar hur ålder påverkar dödlighet. I en Cox regression där ålder är den enda prediktorn skulle baseline hazard vara den risk som människan har vid ålder = 0 år. Efter födseln tillkommer risk allteftersom åldern ökar. (2) Föreställ dig att vi istället studerar hur blodtryck påverkar dödlighet. I en sådan modell skulle baseline hazard vara individens risk vid blodtryck = 0, vilket inte är biologiskt meningsfullt (ingen levande person har blodtryck = 0). Detta innebär att baseline hazard är individens risk när alla prediktorer ställs till 0, vilket är detsamma som att modellen saknar prediktorer. Baseline hazard kan alltså betraktas som risken vid "utgångsläget".
x1, x2 ... xk är de prediktorer (kovariater) som används för att modellera en individs hazard function. Samlingen av prediktorer liknar således en vanlig multipel (linjär) regression. Prediktorerna kan vara kontinuerliga eller kategoriska variabler. Som framgår av formeln ovan så är hela samlingen av prediktorer exponentierade (e).
Cox modell innebär alltså att hazard vid tidpunkt t är produkten av h0(t) och exponenten (e) av prediktorernas sammanlagda effekt. I nästa steg dividerar vi båda sidor om likamedtecknet med baseline hazard och dessutom logaritmeras båda sidor. På höger sida om likamedtecknet försvinner h0(t)och exponentieringen försvinner. På vänster sida om likamedtecknet kvarstår den naturliga logaritmen av h(t)/h0(t).
Den vänstra sidan av ekvationen är individens hazard (risk) och den högra sidan är en vanlig linjär regression. Detta förfarande är smått genialt eftersom vi nu har anlänt i en ekvation som låter oss studera överlevnaden som en linjär funktion av individens prediktorer. Det var Sir David Cox som lade fram de matematiska bevisen för detta och han framhöll att ekvationen endast stämmer om hazard är proportionerlig. Cox Proportional Hazards Model är synonym för Cox regression. Proportional hazard innebär att ratio (kvoten) mellan två individers hazard function skall vara konstant över tid. Detta gäller för alla karaktäristika som definierar individerna i studien. Ett exempel följer. Om vi studerar dödligheten i Göteborg och inkluderar diabetes som en prediktor i modellen, så måste kvoten mellan diabetikers och icke-diabetikers hazard function vara konstant under hela uppföljningen. Om det är 3 gånger ökad risk för död för diabetiker i början av uppföljningen så skall det vara lika hög risk (3 gånger) för diabetiker under hela studiens uppföljning. Förklaringen till detta kommer av nästa ekvation, där hazard function för två individer jämförs:
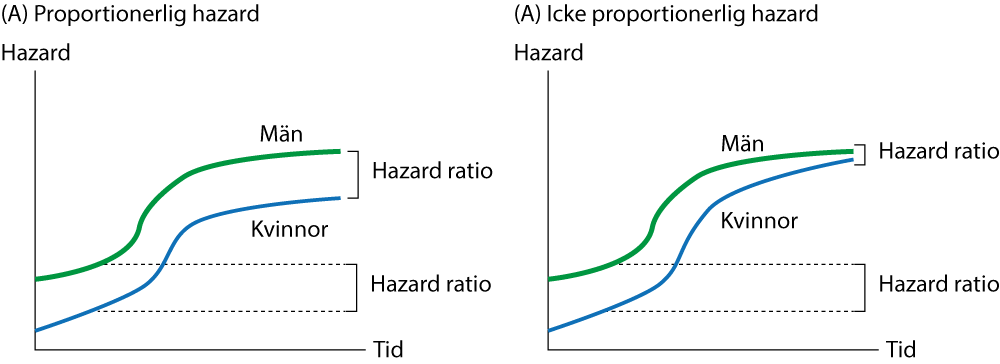
Denna kvoten mellan två hazard functions är hazard ratio (HR). Det är alltså den relativa skillnaden i risk för individ 1 jämfört med individ 2. Eftersom h0(t) ingår i både täljaren och nämnaren så utgår den fullständigt. I ekvationen finns inte heller tid. Således är det endast värdena på prediktorerna som skiljer individ 1 och individ 2; varken baseline hazard eller tid kan påverka hazard ratio, som därför är konstant mellan individ 1 och individ 2. Det inebär också att om någon av prediktorerna (x1, x2 ... xk) skulle ha en varierande effekt över tid, så kommer kravet om proportional hazards inte vara tillfredsställt och modellen blir ogiltig. I Figur 4 illustreras proportional hazards och non-proportional hazards.
Hazard ratio (hazardkvot)
Hazard ratio beräknas genom att dividera hazard för en individ med hazard för en annan individ (se formel ovan). Hazard ratio beräknas när en händelse inträffar. Om en händelse inträffar vid tidpunkt t så beräknas hazard ratio genom att dividera hazard för individen som erfarde händelsen med hazard för övriga som klarade sig fram till tidpunkt t utan att erfara händelsen. Baseline hazard utgår (förklarat ovan) från kvoten likaså är tidpunkten irrelevant eftersom alla individer jämförs vid samma tidpunkt. Det som karaktäriserar individerna blir således deras prediktorer (x1, x2 ... xk). Således kan effekten av prediktorerna analyseras! I en Cox regression beräknas vi alltså koefficienterna för prediktorerna (x1, x2 ... xk), vilket är dessa prediktorers inverkan på överlevnaden. Den hazard ratio som erhålls när två individers hazard divideras är logaritmerad, vilket också gör att den är svårtolkad. För att ordna detta så exponentieras koefficienten. Om regressionskoefficienten är 0.5 så blir den exponerade koefficienten e0.5 = 1.65. När vi använder termen hazard ratio så referar vi egentligen till den exponentierade koefficienten!
Tolkning av hazard ratio
- För en kontinuerlig prediktor så är hazard ratio den ökning/minskning i hazard som följer när prediktorn X ökar med en enhet.
- För en kategorisk variabel så är hazard ratio skillnaden i hazard mellan två (eller flera grupper) där en av grupperna är referensgrupp.
För att bättre förstå detta behöver vi ett exempel och vi skapar själva detta exempel i R.
R kod
library(survival)
# Vi skapar en Cox regression som studerar hur age, sex och meal.cal påverkar dödligheten
modell2 <- coxph(Surv(time, status==2) ~ age + factor(sex) + meal.cal, data = lung)
# Vi installerar och aktiverar ett paket som skapar snygga tabeller med resultaten
install.packages("forestmodel")
library(forestmodel)
forest_model(modell2)
Resultat från modellen
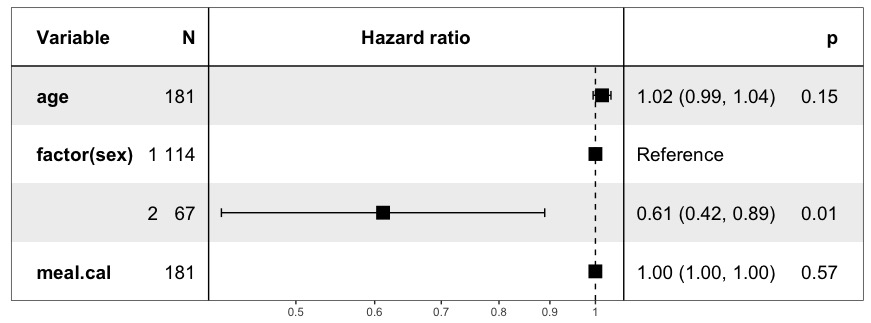
Denna modellen har alltså tre prediktorer: age, sex och meal.cal. Sex är en kategorisk prediktor med nivåerna 1 (män) och 2 (kvinnor). Age och meal.cal är kontinuerliga prediktorer. Hazard ratio presenteras både med en graf (mitten) och siffror (näst sista kolumnen). Notera att hazard ratio presenteras tillsammans med sitt 95% konfidensintervall. Exempelvis så är hazard ratio for sex 1.02 med ett 95% konfidensintervall som sträcker sig från 0.99 till 1.04. Den sista kolumnen är P-värdet som indikerar om prediktorn har ett statistiskt signifikant samband med dödligheten. Detta är en typisk presentation av en Cox regression. Kolumnen "N" anger hur många individer som ingår i varje kategori (denna kolumnen kan ignoreras). Härnäst följer tolkningen av resultaten.
- Hazard ratio för sex: I tabellen är sex presenterat på två rader. Detta beror på att sex är en kategorisk variabel med två nivåer. Vi får inga koefficienter (hazard ratio) för män, vilket beror på att män är referenskategorin. För alla kategoriska variabler finns alltid en referenskategori med vilken de övriga kategorierna skall jämföras. Vi får således hazard ratio för kvinnor och resultatet är 0.61 med konfidensintervall som sträcker sig från 0.42 till 0.89. Detta är hazard ratio för kvinnor när de jämförs med män. Hazard ratio är mindre än 1, vilket innebär att kvinnor har lägre risk än män. Om vi subtraherar 1 från 0.61 och multiplicerar skillnaden med 100 så får vi riskskillnaden i procent; (0.61–1.0)×100 = –39%. Kvinnor har, jämfört med män, 39% lägre risk för död. Detta är alltså "punktestimatet" och det finns en viss osäkerhet i det. Därför får vi även ett 95% konfidensintervall, som indikerar att kvinnor har (med 95% säkerhet) mellan 58% och 11% lägre risk än män.
- Om vi skulle ha en prediktor med fler än 2 nivåer så skulle tolkningen vara densamma; en kategori är referens och övriga kategorier jämförs med den.
- Konfidensintervallet för kvinnor omsluter inte värdet 1.0. Om hazard ratio är 1.0 så ju kvotens täljare och nämnare lika stor, vilket innebär att det inte är någon skillnad mellan grupperna. Det innebär att ett konfidensintervall som omsluter 1.0 indikerar att man inte med 95% säkerhet kan säga att det finns en skillnad mellan grupperna. För kvinnors vidkommande så ingår inte 1.0 i konfidensintervallet, så vi kan med 95% säkerhet säga att det finns en skillnad mellan män och kvinnor. Detta styrk av P-värdet (0.01) som anger att kön är en statistiskt signifikant prediktor.
- Denna modellen inkluderar alltså även age och meal.cal, utöver sex. Då är effekten av sex justerad för effekten av de övriga prediktorerna i modellen (de övriga prediktorerna "hålls konstanta").
- Age (ålder) är en kontinuerlig prediktor. Därför tolkas hazard ratio som ökningen i hazard för varje enhet ålder ökar. I denna studien var ålder mätt på skalan år, så hazard ratio är ökningen i hazard för varje år deltagarna blir äldre. Resultatet blev 1.02 med konfidensintervall från 0.99 till 1.04. Efter hazard ratio (punktestimatet) är 1.02 så betyder det att för varje år deltagarna blir äldre så stiger risken för död med 2%. Man kan lätt beräkna hur mycket risken stiger på 15 år genom beräkningen 1.0215, vilket ger hazard ratio på 1.35 (dvs 35% ökad risk). I detta fall omsluter dock konfidensintervallet 1.0, eftersom intervallet sträcker sig från 0.99 till 1.04 och därmed kan vi inte säkert säga att ålder har en effekt. Detta påstående styrks av P-värdet som är 0.15 och därmed inte signifikant.
I Cox regression är alltså sambandet mellan prediktorn och hazard linjärt. Modellen är dock inte helt parametrisk eftersom det finns en baseline hazard. Cox regression är således en semi-parametrisk modell.
Konfidensintervall och P-värden för hazard ratio
I R och all annan statistisk mjukvara erhåller man automatiskt standarderror (SE), p-värden och konfidensintervaller när man skapar modellen. Konfidensintervallet är ett såkallat Wald intervall eftersom man använder estimat direkt från modellen för att beräkna intervallet.
Nedre intervall: HR – 1.96×SE
Övre intervall: HR + 1.96×SE
Där HR är Hazard ratio och SE är standard error.
Detaljer om proportional hazards
Proportional hazard kan också förklaras genom interaktioner mellan en prediktor och tid. Om en prediktor uppfyller kriteriet för proportional hazard så skall det inte finnas någon statistiskt signifikant interaktion mellan den prediktorn och uppföljningstid (survival time). Man kan således skapa en interaktionsterm (prediktor×uppföljningstid) och utvärdera om den är statistiskt signifikant. Om interaktionen inte är signifikant så innebär det att prediktorn utövar samma effekt på hazard function vid alla värden på t (uppföljningstid) och då är kriteriet för proportional hazard uppfyllt. Om interaktionen däremot är signifikant så innebär det att effekten av prediktorn varierar över tid och då strider den variabeln mot antagandet om proportional hazard. Det finns ytterligare sätt att utvärdera proportional hazards, och dessa är som följer:
- Utvärderig av Schoenfeld residualer
- Visualisera log(-log S(t)) mot t
Egentligen bör man föredra de två sistnämnda metoderna framför interaktionstermer. I R finns enkla funktioner som presenterar både Schoenfeld residualer och grafer över log(-log S(t)) mot t.
Stratifiering (den stratifierade Cox modellen)
Cox regressionen erbjuder möjligheten att justera för variabler som inte ingår i modellen och detta görs genom att stratifiera. Man får inte förväxla stratifiering vid Cox regression med stratifiering vid vanlig linjär (multipel) regression.
Vid vanlig linjär (multipel) regression så innebär stratifiering att man skapar separata modeller utifrån en kategorisk variabel. Exempel följer. Ponera att vi studerar hur ålder påverkar blodtryck och vi har även information om vikt. Om vi vill veta hur ålder påverkar blodtryck i olika viktkategorier så kan vi stratifiera analysen genom att göra en regression för normalviktiga, en regression för överviktiga och en regression för personer med fetma. Detta är alltså tre separata modeller som ger separata koefficienter för ålder.
Vid Cox regression kan stratifieringen hanteras annorlunda. Cox modell tillåter oss stratifiera data (patienterna) utifrån en kategorisk variabel. Baseline hazard tillåts variera mellan dessa strata. Modellen kan sedan estimera en sammanlagd (kumulativ) effekt av ålder i alla strata. Då erhåller vi endast en koefficient för ålder, istället för separata koefficienter i varje strata. Man kan säga att effekten av ålder "poolas" (sammanvägs) i alla strata.
Det finns flera situationer då det är klokt att statifiera modellen. Exempel följer. Om en variabel strider mot antagandet om proportional hazard så kan man kategorisera variabeln till två eller flera lämpliga nivåer och stratifiera modellen på den variabeln. Då har man justerat för variabeln och man behöver inte oroa sig för att den strider mot proportional hazards. Nackdelen är att man inte erhåller några regressionskoefficienter för variabeln (men om den ändå inte är av intresse för analysen så är detta ingen större nackdel.