Strategier för att bygga statistiska modeller för prediktion, estimera effekt eller testa hypoteser

I denna kursen har vi diskuterat ämnen som studiedesign och hypotestester. Vi har även diskuterat principer för de vanligaste statistiska modellerna (regressionsanalys) och deras användningsområden. För att knyta ihop säcken behövs en diskussion om strategier och metoder för att bygga en statistisk modell. Med statistisk modell avses alla statistiska analyser vars syfte är att belysa samband mellan variabler.

De frågor som ofta uppstår när man bygger en statistisk modell är som följer:

• Har jag valt rätt modell? I de föregående kapitlen har vi diskuterat olika modeller och deras användningsområde. I den absoluta merparten av fallen använder man regressionsmodeller (t ex linjär [multipel] regression, logistisk regression, Cox regression osv)  för att studera forskningsfrågan och den fortsatta diskussionen kretsar därför kring strategier för regressionsmodeller.
• Hur skall jag definiera utfallsmåttet (Y)? Utfallsmåttet skall alltid vara meningsfullt (ur biologiskt och/eller kliniskt perspektiv) och relevant för forskningsfrågan. Oftast är det enkelt att definiera utfallsmåttet men det finns scenarion då det kan vara svårt. Inte sällan aktualiseras frågan om att kategorisera en kontinuerlig variabel för att bättre belysa forskningsfrågan. Oavsett scenario så skall utfallsmåttet alltid vara meningsfullt och belysa forskningsfrågan.
• Vilka variabler skall jag inkludera i modellen (variabelselektion)? Att välja rätt statistisk modell och definiera ett meningsfullt utfallsmått är oftast enkelt. Att välja vilka variabler som modellen skall innehålla ger oftast mer huvudbry. Denna diskussionen kommer diskutera detta i detalj.
• Hur skall modellen specificieras? När man vet vilka variabler som skall inkluderas i modellen så blir nästa fråga hur modellen skall specificeras. Exempel på vanliga frågor som uppkommer listas nedan:
  • Skall jag kategorisera en kontinuerlig variabel?
  • Skall jag inkludera interaktionstermer i modellen, och i så fall vilka?
  • Om en prediktor inte är statistiskt signifikant, skall jag exkludera den från modellen?
  • Uppfyller modellen (och respektive prediktor) de antaganden som krävs för att använda regressionsmodellen?

1. Hitta lämplig analysmetod: hypotestester, regressionsanalys eller träbaserade metoder

Ponera att du undersöker sambandet mellan alkoholkonsumtion och koloncancer. För detta ändamål har du en studiepopulation som inkluderar 500 personer med koloncancer samt 500 kontrollpersoner utan koloncancer. För samtliga 1000 personer har du uppgifter om cirka 50 olika variabler som karaktäriserar deras hälsa, levnadsvanor osv. Alkoholkonsumtion är en kontinuerlig variabel som indikerar antal glas man dricker per månad. Personer med koloncancer angav alkoholkonsumtion innan cancerdiagnos och symptom uppenbarades. Forskningsfrågan är alltså:

Finns det ett samband mellan alkoholkonsumtion och koloncancer?

Det finns olika metoder för att belysa denna forskningsfrågan men oavsett metod bör man alltid ta avstamp i en hypotes. Statistiska modeller som utmynnar i P-värden, koefficienter och konfidensintervaller tar alltid avstamp i en nollhypotes, som säger att det inte finns någon skillnad i alkoholkonsumtion mellan patienter som har respektive inte har koloncancer. Nollhypotesen (H₀) är alltså:

H₀: Det finns ingen skillnad i alkoholkonsumtion mellan patienter som har respektive inte har koloncancer.

Du kan välja att belysa nollhypotesen med något av följande alternativ:

1. Ett enkelt statistiskt test – Om alkoholkonsumtion är en kontinuerlig normalfördelad variabel så kan ett t-test avgöra om konsumtionen är densamma i de båda grupperna. Analysen ger oss ett P-värde (sannolikhet) för att nollhypotesen är korrekt. Om P-värdet är mycket litet (<0.05) så förkastar vi nollhypotesen och tror istället att det finns en skillnad mellan grupperna. Statistiska tester är oftast enkla och bygger på få antaganden. Dessvärre är informationsutbytet tämligen litet eftersom man endast erhåller ett P-värde.
2. Regression - En regressionsmodell ger större möjligheter att karaktärisera sambandet mellan alkoholkonsumtion och koloncancer. Om utfallsmåtet (Y) är alkoholkonsumtion så kan linjär regression användas för att utröna om koloncancer-status (ja/nej) är en statistisks signifikant prediktor. Då erhåller vi också ett P-värde men därutöver även koefficienter med konfidensintervall. Med dessa kan vi uttala oss om hur starkt sambandet är och dessutom kan vi utifrån värden på X predicera (förutsäga) värdet på Y.

Oavsett vilken metod du väljer så kommer resultatet – avseende P-värdet och slutsatsen – vara densamma. T-testet är nämligen ekvivalent med linjär regression med en prediktor. Med samma analogi finns det matematiska samband mellan flera andra tester och regressionsmodeller.

Man bör alltid eftersträva enkelhet utan att förlora värdefull information. Det innebär att i valet mellan enkla tester och regressionsmodeller måste man göra en noggrann avvägning. Statistiska tester är enkla, bygger på få antaganden men ger begränsad information. Regressionsmodeller är mer komplicerade, bygger på fler antaganden och kräver en betydligt större arbetsinsats. I gengäld ger regressionsanalys mer information.

Regressionsmodeller kan alltså användas för att testa hypoteser och i detta avseende finns många likheter med vanliga statistiska tester. Det innebär också att flera fallgropar som gör sig gällande för statistiska tester även måste beaktas vid regressionsanalys. Exempelvis kan nämnas att man alltid avråder från att testa för många nollhypoteser (t ex med t-test)  i jakten på statistisk signifikans; detta ökar nämligen sannolikheten för att hitta falska signifikanser. Av samma anledning bör man inte testa för många prediktorer i en regressionsmodell.

Stickprovets storlek (sample size) är av betydelse både för statistiska tester och regression. Inte skriver forskare att de beslutade att använda t-test istället för linjär regression eftersom stickprovet var litet. Detta är en fadäs eftersom kravet på sample size är lika stort för både tester och regression.

Tree-based methods, ensemble methods, machine learning (ML) och artificiell intelligens (AI)

På senare år har regressionsanalys fått konkurrens av machine learning som innebär att man använder olika algoritmer för att analysera data. De första populära metoderna för machine learning var de så kallade träbaserade metoderna (tree-based methods). Dessa är enkla att förstå, vilket också är en förutsättning för att förstå mer komplicerade algoritmer inom machine learning. Idag används machine learning mycket flitigt inom alla sektorer, från medicin till verkstadsindustri. Machine learning inbegriper alltså en lång rad metoder där man nyttjar mer eller mindre komplicerade algoritmer för att analysera data. Machine learning ingår i ramverket artificiell intelligens (AI). Flera av de mest populära metoderna inom machine learning liknar faktiskt människans tillvägagångssätt vid beslutsfattande.

Träbaserade metoder (tree-based models) analyserar alltså data på ett sätt som liknar människans tillvägagångssätt för att fatta beslut eller ställa diagnoser (klassificera). Dessa metoder (varav den mest populära är random forest) kan användas för att predicera både kontinuerliga och kategoriska utfallsmått (Y). Prediktorerna kan likaledes vara kontinuerliga och/eller kategoriska. Det innebär att träbaserade metoder kan användas (i princip) i samma situationer som man använder regressionsanalys. Träbaserade metoder använder algoritmer som partitionerar data. Partitionering innebär att den ursprungliga datamängden (individerna som man studerar) delas in i mindre och mindre grupper med hjälp av kriterier som finns i algoritmen. Här följer ett enkelt exempel på hur data kan partitioneras:

Förklaring till bild ovan

1. Algoritmen börjar med att dela upp populationen efter kön, vilket innebär att män och kvinnor hamnar i separata grupper.
2. Algoritmen fortsätter genom att dela in grupperna efter ålder.
   • Algoritmen beräknar (med hjälp av fördefinierade kriterier) att ålder 65 kan användas som gräns för att skapa två nya grupper och observationerna som hamnar i de nya grupperna är så lika varandra som möjligt (algoritmen eftersträvar detta).
3. Algoritmen fortsätter sedan genom att särskilja observationer som är födda i Sverige respektive utomlands.
4. och så vidare

Algoritmen analyserar alltså variablerna (prediktorerna) som beskriver individerna och tillämpar sedan ett kriterium för att partitionera individerna i olika grupper. Ovanstående diagram kallas även decision tree. Idag har denna tekniken blivit mycket sofistikerad. Nya metoder (t ex random forest, gradient boosting etc) fungerar genom att bygga ett mycket stort antal träd (upp till flera tusen). Då konstrueras varje träd genom att algoritmen slumpmässigt väljer ut en andel av alla individer (t ex en tredjedel av individerna) samt en andel av alla prediktorerna (t ex en tredjedel av alla prediktorer). Trädet byggs sedan med hjälp av de individer och prediktorer som valdes ut. Denna process upprepas hundratals eller tusentals gånger, vilket innebär att man konstruerar många olika träd.

Träden kan sedan användas som prediktionsmodeller eftersom man kan ta en ny individ (som inte deltagit i uppbyggnaden av träden) och "föra individen genom alla träden" och på så vis se var i träden individen hamnar. Om man exempelvis undersöker risken för att dö så kan algoritmen beräkna risken för att den individen skall dö baserat på var i träden individen tenderar att hamna; algoritmen har nämligen noterat vilka platser i träden som är associerade med död. Metoder som kräver att man konstruerar många träd kallas ensemble metoder (ensemble methods).

De allra flesta machine learning metoder är utmärkta för att (1) predicera Y och (2) kartlägga hur starkt sambandet är mellan X och Y. Dessa metoder är också användbara för att upptäcka och beskriva icke-linjära samband och interaktioner mellan prediktorerna.

Den fortsatta diskussionen kretsar kring regressionsanalys.

2. Definera syftetmed regressionen: prediktion, effektestimering eller hypotestesting?

För att estimera effekten av en prediktor (X) samt för att predicera ett utfall (Y) givet värdet på en eller flera prediktorer, så behövs regression. Det finns tre anledningar till att använda regression och de är som följer:

1. Effektestimering – Att estimera effekten av en eller flera prediktorer som är av intresse. Effektestimering innebär att man har en prediktor (eller flera) som är av särskilt intresse (eng. predictor of main interest) och avser karaktärisera sambandet mellan prediktorn och utfallet. Det är möjligt att skapa en modell som enbart inbegriper utfallet (Y) och prediktorn (X). Oftast brukar man dock behöva justera för andra prediktorer för att reducera bias (confounding). För att bygga dessa modeller krävs kunskap (klinisk, epidemiologisk, molekylärbiologisk etc) om sambandet mellan prediktorn och utfallsmåttet. Sådan kunskap får avgöra om modellen är korrekt specificerad eller om, exempelvis, justering behövs för andra prediktorer.
2. Prediktion – Att (förutsäga) predicera ett utfall. I studien med koloncancer hade vi information för totalt 50 variabler och det är sannolikt att många av dessa kan användas för att predicera risken för koloncancer. Om syftet är att förutsäga vem som kommer utveckla koloncancer så är prediktion syftet med regressionen. Dessa modeller kräver både kunskap om ämnet och därutöver flera steg där modellen kalibreras, valideras och justeras för att säkerställa att prediktionen är så bra som möjligt med så få variabler som möjligt. Syftet med de allra flesta prediktionsmodeller är att de skall användas på bred front och då måste modellen vara tillförlitlig, ha hög precision och dessutom vara sparsam (eng. parsimonious) avseende antalet prediktorer i modellen. Ju fler prediktorer (och ju mer svårtillgängliga prediktorerna är) desto mindre användbar är modellen.

Samma regressionsmodell kan användas för både prediktion och effektestimering. En regressionsmodell estimerar alltid effekten av prediktorerna (regressionskoefficienterna, β) och likaså kan man alltid predicera när man har en färdig modell. Prediktion för en given patient/observation görs genom att mata in patientens/observationens värden för de variabler som ingår i modellen. Då kan ett predikterat (beräknat) värde på utfallsmåttet erhållas.

3. Planering av regressionsmodellen

För regressioner vars syfte är att estimera effekt av prediktorn X, så bör man säkerställa att det faktiskt är meningsfullt att skatta effekten av X. Det finns givetvis olika grader av "meningsfull" i detta sammanhang. Att estimera effekten av LDL på risken för akut hjärtinfarkt kan tyckas meningslöst idag då det har publicerats tiotusentals artiklar med den frågeställningen. Detta kräver alltså en individuell bedömning och kunskap om området är förstås avgörande.

Om syftet är att predicera ett utfall (Y) så bör även detta vara meningsfullt. Det kräver som regel att andra forskare/kliniker skall kunna använda modellen för att förutsäga något negativt (död, återfall av cancer, hjärtattack, insjuknande i reumatism osv) och på så vis kunna förebygga händelsen. Alla utfallsmått behöver inte vara så dramatska som död och hjärtinfarkt. Mjukare utfallsmått kan vara lika relevanta i sitt sammanhang.

Om syftet är prediktion så bör man också förvissa sig om att variablerna som ingår i den slutliga modellen är lättillgängliga. Erinra att om information saknas för en enda prediktor i en modell, så kan prediktionen inte erhållas (för att predicera Y så måste information om alla prediktorerna X finnas). Det innebär att ju fler och ju dyrare (att erhålla) prediktorer en modell innehåller, desto mindre kommer den användas.

Om syftet är prediktion så måste man säkerställa att datamängden (antal observationer) är tillräckligt många för att man skall kunna utbilda och validera modellen. Modellen utbildas som regel på ca 80% av observationerna, vilket lämnar 20% av observationerna för att validera modellen. Detta förfarande säkerställer att man inte överskattar modellens precision. En modell kan förväntas ha god precision i datamängden som den utbildades med, och betydligt sämre precision i en datamängd som inte ingick i utbildning av modellen.

Oavsett syfte så måste man förvissa sig om att man har alla viktiga prediktorer. Detta är sällan ett problem i en studie som designats och genomförts för ett specifikt ändamål. Inte sällan är det dock så att man försöker besvara många frågeställningar med samma studiepopulation eller kombinationer av populationer och då kan detta bli ett problem. Om man saknar prediktorer som är viktiga för utfallsmåttet, och därmed "nöjer sig med de man har", så introducerar man bias, eftersom det inte är säkert att samma effekter skulle observeras om de viktiga prediktorerna hade ingått i modellen.

Det är fundamentalt att den population man använder för analysen är representativ för populationen som man avser uttala sig om (se statistisk inferens). Om man avser uttala sig om behandlingseffekt av statiner och studerar en population med medelålder 65 år, så bör man i princip inte uttala sig om effekten på 40-åringar.

Missing data och multiple imputation

Missing data behöver beaktas. Missing data innebär att värdet på en variabel saknas. Alla studier innehåller missing data och detta gäller både prediktorer (X) och utfallsmått (Y). Erinra att om värdet saknas för en variabel (X eller Y) i en statistisk modell så kommer den individen (som saknar värde) inte inkluderas i modellen. Det gör att modellen tappar en observation och därmed styrka. Alla statistiska modeller blir bättre ju fler observationer som ingår i modellen. Om missing-frekvensen är låg (<5%) för en variabel så är detta sällan ett problem men allteftersom missing-frekvensen stiger så påverkas modellens validitet. Man bör således förvissa sig om hur vanligt missing är (för varje variabel) och undersöka om de personer som utesluts från modellen skiljer sig från de som är kvar i modellen. Sistnämnda kan göras genom att skapa en deskriptiv tabell där karaktäristika för de som ingår respektive exkluderas från modellen jämförs. Om karaktäristika inte skiljer sig nämnvärt så kan man anta att missing är missing at random, vilket innebär att värdet saknas av en ren slump. Om så är fallet så påverkar inte missing modellens validitet. Det är också möjligt att imputera missing, vilket innebär att man fyller i alla saknade värden med lämpliga värden. Imputation bör göras med metoden multipel imputation, vilket diskuteras senare.

Prospektiv vs. retrospektiv studiedesign

En prospektiv studie ger bättre möjligheter att definiera och samla information om variabler och utfallsmått. För en retrospektiv studie är detta betydligt svårare och inte sällan tvingas man acceptera informationen i dess tillgängliga form.

4. Vilka riskdimensioner är tillgängliga?

Denna punkt är mest relevant för modeller som avser uttala sig om risken för en händelse, oavsett om syftet är prediktion eller effektestimering. Risk är oftast en multifaktoriell historia och det är önskvärt att flera dimensioner av risk ingår i en riskmodell. Det innebär att en modell som enbart inkluderar biomarkörer sannolikt är undermålig. Följande dimensioner kan betraktas som viktiga för risken för en händelse:

• Ålder och kön – Dessa variabler är i princip alltid starka prediktorer och bör alltid medbringas i en riskmodell.
• Relevanta biomarkörer.
• Variabler som beskriver det omedelbara (akuta) hälsotillståndet.
• Variabler som beskriver sjukdomar och riskfaktorer som individen har.
• Variabler som beskriver individens fysiska kondition och kapacitet.
• Psykologisk, kognitiv och psykosocial status.
• Variabler som beskriver etnisk, socioekonomisk och kulturell tillhörighet.
• Quality of life.
• Patientens inställning till sjukdom och hälsa.

Efter Iezzoni (2006).

Att ha tillgång till alla dessa dimensioner är en ovanlighet och oftast får man nöja sig med färre dimensioner.

5. Hantering av variabler (prediktorer): kategoriska, kontinuerliga

När man samlar in data och därefter skapar statistiska modeller så skall man alltid eftersträva att använda kontinuerliga variabler. En kontinuerlig variabel innehåller alltid mer (oavsett modell) information än en kategorisk variabel och det är som regel felaktigt att kategorisera en kontinuerlig variabel. Trots detta kategoriseras ofta kontinuerliga variabler utan att det är berättigat. Det finns dock scenarion då det är berättigat att kategorisera en kontinuerlig variabel. Ponera att vi undersöker hur BMI påverkar risken för diabetes och vi skapar en logistisk regression där BMI är prediktorn och diabetes (ja/nej) är utfallet. Om BMI är en kontinuerlig variabel så kommer regressionskoefficienten indikera hur mycket risken för diabetes ökar för varje enhet BMI stiger. Om vi hellre vill uttala oss diabetesrisken för överviktiga så måste vi BMI-variabeln (BMI ≥25 definieras som övervikt). I detta fall är det frågeställningen som formulerar prediktorn och i det fallet är det meningsfullt att kategorisera BMI. För övrigt bör man använda kontinuerliga variabler när det är möjligt.

Det innebär också att prospektiva studier bör samla in data som kontinuerliga variabler i den mån det är möjligt. Då kan man kategorisera variablerna i ett senare skede.

Antagandet om linjäritet: relaxering med restricted cubic splines och polynom

Linjära modeller dominerar analyser som görs för effektestimering och prediktion. Den linjära modellen bygger på antagandet att det finns ett linjärt samband mellan prediktorn X och utfallet Y (Figur 1A). Detta antagande är en bekvämlighet, eftersom linjär regression är betydligt enklare att hantera än icke-linjära regression.  Faktum är dock att naturen sällan är helt linjär och det är naivt att utgå ifrån att sambanden är linjära. Anledningen till att forskare oftast nöjer sig med linjära funktioner är för att de erbjuder en acceptabel approximation av verkligheten. Det finns anledning att alltid utforska om sambandet är linjärt och anledningen till detta är som följer:

• Om sambandet är linjärt så kan detta bekräftas och modellens validitet ökar när variablerna är korrekt specificerade.
• Om sambandet är icke-linjärt så kan även det bekräftas och därutöver kan man eventuellt avslöja spännande relationer mellan prediktorn och utfallet. Det kan exempelvis avslöjas att risken för koloncancer inte stiger förrän alkoholkonsumtionen överstiger en viss mängd per dag.

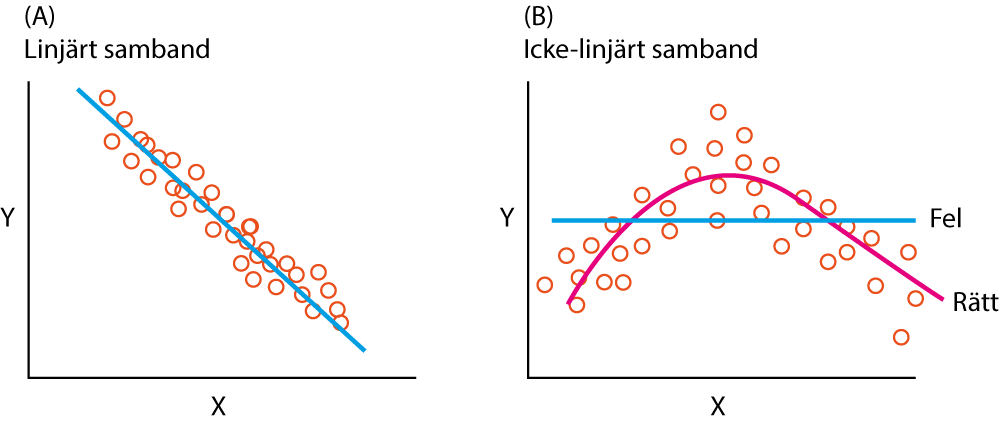
Om sambandet mellan X och Y inte är linjärt så kan det leda till felaktiga slutsatser. I Figur 1B presenteras en linjär regression (blå linje) som leder till den felaktiga slutsatsen att det inte finns något samband mellan X och Y (β = 0 för prediktorn X eftersom regressionslinjen inte har någon lutning). Det behövs en mer flexibel regressionslinje, såsom den röda linjen vilken följer data betydligt bättre. Vi behöver alltså metoder för att testa och relaxera antagandet om linjärtet. Tidigare rekommenderade man ofta transformering av prediktorn X (t ex genom logaritmering) men med befintlig statistisk mjukvara är det numera möjligt att testa och relaxera linjäritets-antagandet på mer sofistikerade sätt.

Att relaxera antagandet om linjäritet innebär att man skapar en modell som inte förutsätter att sambandet mellan prediktorn X och utfallet Y är linjärt. Det enklaste sättet att göra detta är med hjälp av polynom (eng. polynomials). Ett polynom är helt enkelt heltalspotenser av prediktorn X. Om prediktorn X är ålder så finns följande polynom:

• Andragradspolynom: X²
• Tredjegradspolynom: X³
• Fjärdegradspolynom: X⁴

Om man önskar inkludera polynom i en regression så måste alla lägre grader av variabeln också inkluderas. Det innebär att om fjärdegradspolynom (X⁴) för ålder skall inkluderas i modellen så skall även X³, X² och X inkluderas (som enskilda prediktorer). Som regel behåller man polynom vars regressionskoefficienter är signifikanta (P<0.05) eftersom detta är bevis för att det finns en icke-linjär funktion i data.

Polynom erbjuder, jämfört med linjära funktioner, bättre ackomodering till icke-linjära funktioner (böjningar). Dessa funktioner redovisas i Figur 2.

I R specificeras polynomfunktioner på följande vis:

[code lanaguage="r"]

# Laddar survival paketet för att hämta lungcancer-data

library(survival)

data(lung)

# Logistisk regression där död (status==2) modelleras mot kön, ålder samt andragradspolynom av ålder. Andragradspolynomet defineras som framgår nedan ("I" måste anges för att R skall veta att det rör sig om en högre funktion)

fit <- glm(status=="2" ~ sex + age + I(age^2), data = lung, family="binomial") summary(fit)

[/code]

Om koefficienten för andragradspolynomet (age²) är signifikant så indikerar det att det finns en sådan funktion i data (se Figur 2) som kan predikteras med ett andragradspolynom. Polynom har dock flera brister som kan leda till otillfredsställande prediktioner. Splines föredras ofta framför polynom.

Regression splines: linjära splines, cubic splines, restricted cubic splines

En spline är en flexibel funktion som består av flera polynom. Varje polynom representerar ett intervall av fördelningen för prediktorn X och alla polynom är sammankopplade i ändarna.

Den enklaste spline-funktionen är den linjära. En enkel linjär spline innebär helt enkelt att prediktorn X har delats in i intervaller vilket leder till att prediktorn X egentligen delas upp i flera prediktorer. Även om de enskilda intervallerna är linjära funktioner så kan de tillsammans skapa en icke-linjär funktion. I Figur 3 har prediktorn X delats in i 5 intervaller med hjälp av fyra knytpunkter (eng. knots). Antal och placering av dessa knots kan justeras.

En enkel linjär spline möjliggör modellering av icke-linjära funktioner och kräver endast att sambandet mellan X och Y skall vara linjärt inom varje intervall.

Ekvationen för den ursprungliga modellen (utan spline) är som följer:

Y = β₀ + β₁X₁

Om prediktorn X₁ expanderas till en spline med 5 intervaller så blir ekvationen:

Y = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + β₄X₄ + β₅X₅

Cubic splines (CS)

En linjär spline är oftast att föredra framför polynom, men dessväre är linjära splines inte flexibla i knytpunkterna och därför kan böjda/krökta samband inte modelleras optimalt. För att överkomma detta kan man använda cubic splines, som är detsamma som linjära splines men i varje intervall använder man polynom. Detta gör att kopplingarna mellan intervallerna är mjuka och cubic splines är bättre (än linjära splines) på att definiera böjda/krökta samband.

Om en cubic spline har 3 knypunkter (knots) så måste totalt 6 regressionskoefficienter (β₁ till β₆) beräknas. Antal koefficienter som måste beräknas är nämligen k+3, där k är antalet knots. Det innebär att användning av cubic splines blir kostsamt sett till antal frihetsgrader som slösas.

Restricted cubic splines (RCS, natural splines)

Den bästa och mest använda spline-funktionen är restricted cubic spline. Dessa spline-funktioner är som cubic splines men funktionen tvingas vara linjär i svansarna (i början och slutet av prediktorns distribution). Detta ger bättre precision i modellen. Användning av restricted cubic splines bestraffar modellen med k+1 parametrar. Det innebär att om 3 knots används så måste 4 koefficienter beräknas.

Behövs splines?

Om en prediktor X expanderas till en spline-funktion så kan man använda P-värdet för att avgöra om spline-funktionen är nödvändig. Nollhypotesen är att koefficienterna (för de enskilda spline-intervallerna) är lika med 0 och om P-värdet är < 0.05 så är detta osannolikt och då behåller man sina splines.

Hur många knypunkter (knots) behövs?

Om man känner till sambandet mellan prediktorn X och utfallet Y, och vet var det finns kurvaturer och icke-linjäriteter så kan man själv (i mjukvaran R) specificera var knytpunkterna skall placeras. Det är dock ovanligt att man på förhand känner till detta. Lyckligtvis har det bevisats att det inte är avgörande var knytpunkterna placeras (särskilt om man använder många knytpunkter). Man kan med gott samvete placera knytpunkter på jämna avstånd längs variabelns fördelning. I de flesta program (inklusive R) väljer man antalet knytpunkter man önskar använda och då placeras dessa ut på jämna avstånd (med hjälp av percentiler) längs variabelns distribution.

Man använder minst 3 knytpunkter och det är sällan nödvändigt att använda fler än 7 knytpunkter (egentligen är fler än 5 oftast onödigt). Ju fler observationer man har desto fler knytpunkter kan användas. Om sample size är >150 (för linjär regression) kan 7 knytpunkter användas.

Restricted cubic splines kan används för linjär regression, logistisk regression, Poisson regression, Cox regression osv. Restricted cubic splines kan användas i all mjukvara, särskilt i R där tekniken är välutvecklad. Det finns funktioner för att skapa och visualisera splines i R.

Man skall vara frikostig med att använda restricted cubic splines eftersom det är naivt att förutsätta att samband är linjära. Man bör dock pre-specificera sina splines innan modellen byggs. Att föregå detta genom att visualisera samband mellan variabler (t ex med korrelationsdiagram) rekommenderas inte. Man skall vara särskilt frikostig med splines för prediktorer som är starkt relaterade till utfallsmåttet. Det är oftast inte lönt att investera frihetsgrader i variabler med svaga samband med utfallsmåttet.

6. Variabelselektion - att inkludera rätt variabler

Att välja vilka variabler som skall ingå i modellen är svårt. Som regel startar man med ett större antal variabler (kandidatvariabler) av vilka man avser göra ett urval för att behålla de bästa prediktorerna. Detta kan vara ett stort bekymmer. Det finns flera metoder för att välja "rätt" variabler. En del metoder bygger på algoritmer medan andra baseras på undersökarens kunskap om området. Här nedan diskuters de vanligaste och viktigaste metoderna för att välja vilka variabler som skall ingå i modellen.

Stepwise variable selection: backward & forward stepwise selection

Stepwise (stegvis) variabelselektion är en automatiserad process som innebär att mjukvaran bestämmer vilka variabler som skall ingå i modellen. Detta kan antingen göras med forward eller backward stepwise selection.

• Forward selection innebär att modellen startar med 0 variabler och därefter adderas en variabel åt gången. Den adderade variabeln får kvarstanna i modellen om den leder till en bättre precision ("model fit").
• Backward elimination innebär att alla kandidatvariablerna är med i modellen från början. Därefter elimineras en variabel åt gången; den variabel vars eliminering påverkar model fit minst blir exkluderad. Detta upprepas tills inga variabler kan elimineras utan att modellens model fit blir signifikant sämre.
• Bidirectional elimination är en kombination av båda ovanstående.

Dessa metoder skall i princip aldrig användas. Enda gången det är motiverat att använda dem är om undersökaren inte har någon kunskap om området som studeras och ingen sådan person kan konsulteras. Dessa två metoder strider nämligen mot de flesta principer som statistisk inferens bygger på. Konsekvenser av att använda stepwise selection är som följer:

• R² värden är biased (för höga)
• Själva selektionen av variabler baseras på P-värden (signifikanstester) vilket egentligen endast får användas om man har en pre-specificerad hypotes.
• Standard error (SE) är biased (för små).
• Konfidensintervaller är biased (för snäva).
• P-värden blir falskt för små och det finns problem med multipel testning.
• Regressionskoefficienterna är biased (koefficienterna, och därmed effekten, är falskt för stora).

Univariat screening

Många forskare använder univariat screening för att bestämma vilka variabler som skall ingå i modellen. Detta innebär att en variabel i taget testas och om den är statistiskt signifikant så inkluderas den i den slutliga modellen. Detta är också helt fel eftersom variabelselektionen inte skall baseras på P-värden. Dessutom kan det leda till att variabler som endast är signifikanta i närvaron av andra variabler, blir exkluderade. Således kan man förlora viktiga prediktorer med denna metoden.

Andra modeller

Lasso-metoden, Bootstrap-teknik och Bayes faktor kan också användas för att selektera variabler.

Machine learning, särskilt random forest, kan också användas för att identifiera viktiga variabler. Machine learning (random forest) har ett naturligt sätt att kvantifiera varje prediktors styrka och därmed kan man rangordna alla prediktorerna efter deras prediktionsförmåga. Detta blir allt vanligare i kliniska studier och fördelen är att dessa metoder kan hantera ett mycket stort antal kandidatvariabler (hundratals variabler går utmärkt). Dessutom blir slutresultatet inte influerat av undersökarens förutfattade meningar.

Andra metoder, såsom principal component analysis (PCA) kan också användas men random forest har flera fördelar jämfört med dessa.

Kunskap om området

Man bör alltid använda sakkunskap (litteraturen) för att identifiera viktiga samt oviktiga variabler. Sakkunskap är ovärderligt när man bygger statistiska modeller.

7. Overfitting

En regressionsmodel får inte innehålla för många prediktorer. Om modellen innehåller fler prediktorer än vad datamängden möjliggör, så blir modellen overfitted vilket innebär att dess precision kommer att överskattas. I en modell med för många prediktorer kan dessutom en eller flera associationer (mellan X och Y) vara falska. En modell med overfitting är betydligt sämre på prediktion i ett dataset som inte ingick i utbildningen av modellen. Således måste vi begränsa antalet prediktorer som inkluderas i en modell. Modellens reliability är avhängig av att den inte är överbefolkad med prediktorer.

För en linjär regression (kontinuerligt utfallsmått Y) så är sample size avgörande. Ju fler observationer man har desto fler prediktorer kan man inkludera. Om man dividerar antal observationer med siffran 10 så erhåller man en ungefärlig siffra för antal prediktorer som kan inkluderas.

För en Cox regression är det enbart antalet events som dikterar hur många prediktorer som kan inkluderas. I Cox regressionen så är det nämligen enbart vid events som individer kan jämföras (och därmed prediktorernas effekt skattas). Om man dividerar antal events med 10 så erhåller man en ungefärlig siffra för antal prediktorer som kan inkluderas.

I en logistisk regression finns två nivåer på utfallsmåttet. Den nivån som har lägst frekvens används för att bedöma hur många prediktorer som kan användas och detta görs genom att först betrakta en korstabell:

	Cancer	Frisk	Total
Män	2	10	12
Kvinnor	16	6	22
Total	18	16	34

"Frisk" har lägre frekvens än "Cancer". Om antal friska multipliceras med 3 och produkten divideras med 10 så erhåller vi siffra för antal prediktorer som kan inkluderas. I detta fall blir det: (16×3)/10 = 4.8 prediktorer (dvs ∼ 5).

8. Observationer med stark inverkan på modellen

Resultatet (koefficienterna) från en regressionsmodell kan påverkas starkt av enskilda observationer. Detta är en oönskad effekt eftersom varje observation bör bidra lika mycket till modellen. Det finns flera förklaringar till varför en eller ett fåtal observationer har för stor effekt på modellen:

• Det finns för få observationer i relation till modellens komplexitet. Som regel innebär detta att antal prediktorer i modellen är för många i relation till antalet observationer.
• Extremvärden för prediktorn X kan påverka regressionskoefficienten. Patienter som har extremvärden kan (eventuellt) exkluderas om värdet är extremt och inte heller är representativt för populationen som studeras. Det innebär också att värden som inte är  biologiskt plausibla kan exkluderas.
• Vissa observationer har värden (för prediktorerna) som inte överensstämmer med utfallet. Om många sådana observationer finns i populationen så kan detta förändra sambandet mellan prediktorerna och utfallet. Detta bör dock inte leda till exklusion av patienterna eftersom man då riskerar introducera selektions-bias.

Man kan utgå från en variabels distribution för att exkludera patienter som har extrema värden. Detta kräver dock eftertanke och motivering. Det är också möjligt att kvantifiera hur stor inverkan en observation har på modellen. Detta görs genom att beräkna leverage. Det finns färdiga funktioner för detta i R. Leverage definieras som observationens förmåga att påverka modellen.

9. Att jämföra och välja bland två modeller

När man utvecklar en prediktionsmodell så är det obligatoriskt att testa mer än en modell och då tvingas man slutligen välja den bästa modellen. För att göra detta behövs objektiva jämförelsemått.

Erinra att en prediktionsmodell skall utbildas ("tränas") i en datamängd (training set) men utvärderas i en annan datamängd (validation set). Training set och validation set kan hämtas från samma ursprungliga studiepopulation, huvudsaken är att man avsätter en andel av observationerna (oftast 80%) för träning och resten (20%) för validering.

Man kan jämföra två modeller med samma prediktorer om själva modellspecifikationen skiler sig, interaktioner, hur kontinuerliga variabler modelleras etc. Man kan också jämföra modeller som har olika prediktorer; det är vanligt att man försöker bygga modeller med färre antal prediktorer utan att tappa precision. Denna strategi kallas parsimonous modeling och ordet parsimonious betyer "sparsam", vilket syftar till att modellen skall innehålla så få prediktorer som möjligt. En modell med få prediktorer är en enkel modell (få parametrar behöver beräknas); risken för overfitting är mindre och modellen blir enklare att reproducera av andra forskare.

Man kan använda R² och modellens χ² för att utvärdera modellens förmåga (performance). Dessa mått har diskuterats tidigare (Linjär regression). Man kan också använda AIC (Akaike Information Criterion) eller BIC (Baysian Information Criterion). All mjukvara kan beräkna AIC och BIC automatiskt. Ju mindre AIC är, desto bättre är modellens performance. Man kan således utveckla sina modeller i den riktning som minskar värdet på AIC. BIC fungerar på samma vis.

Mer avancerade metoder som cross-validation och bootstrapping diskuteras inte här.

10 . Priciper för effektestimering: modeller som estimerar effekten av en prediktor

1. Modellen behöver inte vara parsimonious.
2. Undersökaren väljer själv, utifrån kunskap om området, vilka prediktorer som skall vara med i modellen.
3. Undersökaren väljer själv, utifrån kunskap om området, hur modellen skall specificeras (interaktioner, splines, stratifiering etc).
4. Det går utmärkt att kvarhålla icke-signifikanta prediktorer om deras närvaro i modellen gör hela modellen mer realistisk.
5. Interaktioner måste beaktas och, där det bedöms rimligt, användas. Man skall inte leta efter interaktioner utan eftertanke.
6. Om predictor of main interest (prediktorn man är särskilt intresserad av) har hög frekvens missing så kan det vara klokt att imputera missing med multiple imputation.
7. Använd splines och relaxera linjäritets-antagandet frikostigt, särskilt för prediktorer som är starka liksom för predictor of main interest.
8. Kategorisera inte kontinuerliga variabler såvida det inte finns en bra anledning till detta.
9. Modellen behöver inte valideras eller kalibreras.
10. Modell skall helst pre-specificeras.

11 . Priciper för effektestimering: modeller som estimerar effekten av en prediktor

• Säkerställ att så mycket data som möjligt finns tillgängligt.
• Kategorisera inte kontinuerliga variabler.
• För överlevnadsanalys (survival analysis) måste uppföljningen var tillräckligt lång för att tillräckligt många events skall inträffa. Power för en överlevnadsanalys beror helt och hållet på antalet events.
• Säkerställ att en hypotes är etablerad innan dataanalysen börjar. Att pre-specificera kandidatprediktorer är viktigt.
• Man får inte använda utfallsmåtte (Y) för att avgöra vilka prediktorer som bör vara med i modellen. Varken med univariat testning, deskriptiva grafer eller andra hypotestester. Kanddiatprediktorer får inte gallras med dessa metoder.
• Om missing för prediktorn X är betydande, överväg multiple imputation.
• Om du exkluderar många individer med missing data bör du undersöka om de med missing samt de som kvarstod i modellen skiljer sig. Detta kan göras med deskriptiva tabeller. Helst skall båda populationerna vara lika.
• För varje prediktor bör du specificera komplexiteten med vilken den skall modelleras. Det är rekommenderat att linjäritet testas med restricted cubic splines. Prediktorer som är starka bör tillägnas splines med fler knytpunkter (knots).
• Reducera antalet prediktorer om de överstiger vad antalet observationer tillåter (se vägledning under punkt 7 ovan).
• Utveckla modellen i ett sub-sample av hela samplet. 80% av observationerna kan användas för träning och 20% för validering.
• Interaktionstermer skall pre-specificeras och inte sökas omotiverat. Uteslut icke-signifikanta interaktioner.
• Använd leverage för att kontrollera om det finns observationer som utövar "för mycket" effekt på modellen.
• Undersök om det finns collinearity med hjälp av VIF (variance inflation factor).
• Använd bootstrap för att validera modellen.

Referenser

Referens 1 nedan har tjänat som den huvudsakligen källan till detta kapitel. Denna bok rekommenderas varmt.

1. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis av Frank Harrell. Springer 2015.
2. Applied Predictive Modeling av Max Kuhn and Kjell Johnson. Springer 2016.
3. Survival Analysis: A Self-Learning Text, Third Edition. David Kleinbaum. Springer 2012.